地理学に学ぶ世界の見方

イントロダクション
講義構成
まとめ

イントロダクション

日時：2023/05/28/日/16:30~18:00
場所：GOALOOK学習塾

講師：土屋武蔵（Tsuchiya Musashi）
GOALOOK学習塾講師
所属：京都大学　経済学部
出身：埼玉県
卒業：高卒認定試験

今回の白熱教室では、geoguessrというゲームを通して地理学的、多角的な視点での世界の見方について学んでいきます！

geogussrというゲームをご存知でしょうか？YouTubeなどでも人気であり、一度は聞いたことがある人も多いと思います。
ジオゲッサーを一言で説明すると、グーグルマップを利用した場所当てゲームです。

グーグルマップのある地点にランダムで落とされ、周りの風景等を頼りにどこに落とされたのかを推測し、推測した場所が正解と近ければ近いほど点数が高くなるというシステムになっています。

今回の白熱教室は、そんなジオゲッサーで遊びながら日常的な風景が少し面白くなるような知識を得て、当たり前を疑いながら楽しみながら思考力を高めようというテーマで行われました。

ここがオーストラリアかアメリカか、判断できるでしょうか？最初は何が何だか分からない生徒でも、講義を終えた後には自信をもってその根拠と共に答えられるようになってもらいました。知識とその使い方次第で、何気ない情報でも世界の見え方が変わることを体験してもらいます。

講義構成

その当たり前は本当に当たり前？

ジオゲッサーは世界中の地域の道路上に完全なランダムで飛ばされます。操作確認もかねて一度何も説明せずにプレイしてもらいましたが、「そんなのどうやって特定するんだ？」「何も情報がない～」と、運任せ半分で推測するしかありませんでした。ゲームはチームごとの対決形式で行いましたが、お互いあまり差はつかず…。

ここで1度目のインプットタイム。最初に載せた写真を例に講義をします。

この写真を見て、何か気づくことや、違和感はないでしょうか？生徒にも改めて確認してもらう時間をとると

・道路標識の単位がマイル表記である
・車が右側通行である

ということが分かりました。日本では当然、道路標識は㎞表記です。実は、道路標識でマイル表記を用いているのはアメリカだけなんです。このことを知っていれば一発でアメリカ！と答えられたんですね。

さらについ当たり前になってしまっている車の左側通行も、実は世界規模でみるとマイノリティなんです。（赤：右側通行青：左側通行）

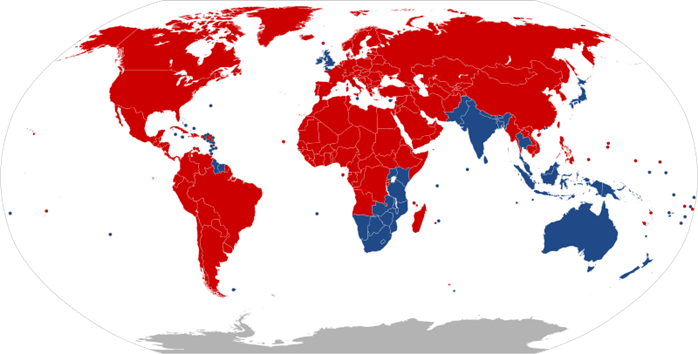
御覧のように、世界では圧倒的に右側通行の方が多いんです。このことだけでも、世界のどこかに落とされた瞬間に道路さえ見られれば多くの選択肢を消すことが出来ますね。

このように日本とは違う世界の文化や当たり前をインプットし、まとめた資料を持ったうえでもう一度プレイしてもらいました。

思考力

「英語を使っているけど、右側通行だからオーストラリアではないよね…。」と学んだことをチームで相談しながら推測していきます。

2度目の対決では、大きく点数に差が出ました。

それぞれに推測の根拠を聞くと、「知識で何択かまでは絞れたけど、そこから先がわからなかったので、なんとなく選んだ」とのこと。その選択肢まではどのチームも絞れているものの、選択肢内で赤道をまたいでおり遠く離れてしまっていて、その中で別々のものを選んだことが点数差の開いた要因だったようです。

ここで2度目の講義を挟みます。もう一度、最初の写真を例にとって考えてみましょう。オーストラリアとアメリカは言語やその土地の広大さなど多くの点で似た特徴を持っていますが、もっとも大きな違いは何でしょうか？

答えはその位置です。当然、アメリカは北半球でオーストラリアは南半球に位置しています。そう考えたうえでもう一度写真の要素を見直してみてください。

画像右下のコンパスを参考にすると、太陽が南寄りに位置していることがわかりますよね。これも我々にとって当たり前の光景ではありますが、実は、北半球特有の景色なんです。（ここでの北半球南半球は北緯南緯23.4度以北以南を指す）

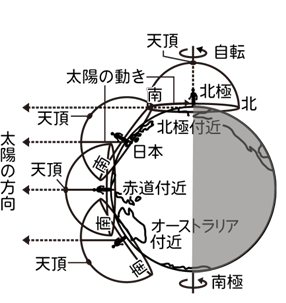
太陽が東から出て、南寄りに上り、西側に沈む。そんな当たりまえの認識すらも、実は世界でみると決して普遍的なことなんかではないことがわかります。南半球の地域の人からすれば、太陽は北側寄りに上るものなんです。

さらに、コンパスを参考にすると西側に山脈が見えていますね。地面に立った時に見える地平線や水平線の境目までの距離はどの程度か知っているでしょうか。

じつはたった5キロほどしか離れていないのです。これは以下の考え方から導かれます。

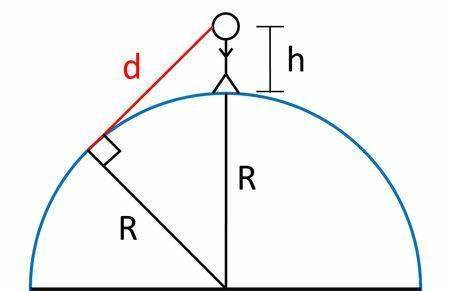
三平方の定理より、地平線・水平線までの距離D(km)は
　　　　D²=(R+H)²-R²
　　　　　=2Rh+h²
よって、
　　　　D=√2Rh+h²
ここで、Rに比べてhは小さすぎるのでh²を無視すると、
　　　　D≒√2Rh
地球の半径Rはおおよそ6000kmなので、地平線・水平線までの距離は、身長hが1.7mだとすると
　　　　D=√2×6000×1.7/1000
　　　　　≒√20
　　　　　≒4.5km

このことを応用し、仮に見えている山が2000ｍほどだとすると、山から約150キロしか離れていないことになります。このことから、これほどの山から東に150キロの地点でこれだけ乾燥した広い土地が広がっているのならば、グレートディバイディング山脈は栄えている東側にあり、それ以外に高い山はあまりないオーストラリアではないのじゃないか、アメリカのロッキー山脈の東側あたりではないか？とまで推測できるかもしれません。

少しレベルが上がりましたが、これらの観点はオーストラリアやアメリカなどの特定の地域の知識ではなく、全世界で応用可能な思考の一つです。一つ一つの国の知識を覚えていくのにはやはり限界があります。これらの考え方だけでは特定には至りませんが、この思考を知識と組み合わせることで、より確度の高い、再現性のある推測が可能になるのです。